[10000印刷√] 角錐 体積 求�� 方 172898-角錐 体積 求め方

 それは、 (三角錐の体積)= (底面積)× (高さ)× です。 三角柱であれば、 (三角錐の体積)= (底面積)× (高さ) で求めることができます。 一方で、図形のてっぺんがとんがっている三角錐の体積を求める場合、必ず をします。 なぜ をしなければならないのかについては、少し厄介な証明が必要なため後で詳しく解説します。 難しければ、気にしなくても大丈夫です。 基本的には、公式だけを覚求め方 1 、 1 辺の長さから正方形の面積を求める ・ 1 辺の長さは 5 ・ 正方形の面積 = 5 × 5 = 25 正四角錐の体積の求め方 1 − 2 2 番目に、正方形の面積に高さと 1 3 を掛けます。 求め方 2 、正方形の面積に高さと 1 3 を掛ける ・ 正方形の面積は 25 、高つまり、四角錐の表面積とは次のように求めることができます。 四角錐の表面積＝底面積 側面積（三角形 つ分） では、実際に問題を解いてみましょう。 次の四角錐の表面積を求めなさい。 （底面は正方形） 展開図を書いて、側面積と底面積を求める

三角錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典

角錐 体積 求め方

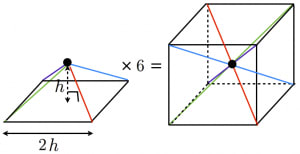
角錐 体積 求め方-TOP > 数学 > 角錐・角錐台の公式(体積) 角錐 計算 辺(a) 辺(b) 高さ(h) 体積 \ V = \frac{1}{3} Sh \ EXCELの数式 A B; 底面積が S S ，高さが h h である錐体の体積 V V を求める公式： V=\dfrac {1} {3}Sh V = 31S h の導出を紹介します。 目次 特殊な四角錐の場合 一般の錐体の場合 積分を用いた証明 特殊な四角錐の場合 底面が一辺 2h 2h の正方形であるような特殊な正四角錐の場合は，立方体を六個に切ることで簡単に V=\dfrac {1} {3}Sh V = 31S h が証明できます。 証明 底面積は S=4h^2 S = 4h2 高さは

体積の求め方 計算公式一覧

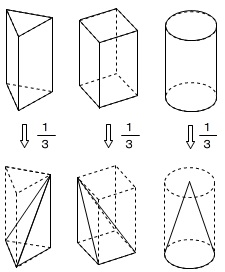
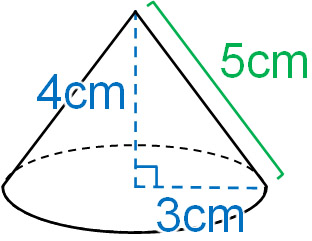
どちらも公式は簡単です。 柱の体積＝底面の面積×高さ 錐の体積＝底面の面積×高さ÷3 錐の高さは、頂点から底面に垂直に引いた線です。 真っ直ぐの線です。 斜めの線ではないので気をつけましょう。 （例題1） 上の図の円錐の体積は何cm²でしょうとなります。よって求めたい円は面積と幅を掛け算して、\(πR^2 dx\)となります。 あとはこの円が高さ\(h\)だけ集まっていることになりますので、体積\(V\)は $$V = \int_0^h πR^2 dx$$ $$ = πR^2 h$$ 円柱の体積の公式である底面積×高さと一致することが分かります。 三角錐さらに、その半分の長さ まで求めておきましょう。 次に、正四角錐の高さを含む こちらの直角三角形に注目します。 すると、先ほど求めた ㎝ の辺を用いて 三平方の定理から高さを求めることができます。 ようやく正四角錐の高さが求まったので

四角錐や五角錐の体積の求め方 忘れている人が割といるので確認しておきます。 柱体と錐体の体積の求め方です。 \(\,\color{red}{(柱体の体積)=(底面積)\times (高さ)}\,\) です。 これは、底面の形に関係なく同じです。 三角柱でも四角柱でも円柱でも同じ。 算数では たて 横 高さ 体積 た て × 横 × 高 さ = 体 積 と習いますが、底面積に高さを掛ければOKです。 やってる計算は同じですよ。 角錐と円錐の体積 角錐と円錐の体積も同じ公式です。 底面積を S 、高さを h とすると、体積 V は以下の公式になります。 V = 1 3 S h 公式に 1 3 が付いている理由は、高校数学で積分を習うとわかります。 難しい計算なので、今は無理矢理 1 3 が付くと 円錐の体積の求め方がわかる3つのステップ 円錐の体積の求め方 はつぎの3ステップをで計算できちゃうよ^^ つぎの例題をときながらみていこう！ 半径3cm、高さ10cmの円錐の体積を計算して^_^ Step1 円錐の「底面積」を計算するっ！ まずは円錐の底面積を計算してみよう。 円錐の底面は「円」になっているね。 ってことは、 円の面積の公式 をつかって

角柱・角錐・円柱・円錐の体積の求め方がわかりません。公式を教えてください。 進研ゼミからの回答 立体の体積はこれから先も利用するので，それぞれしっかり覚えておきましょう。 ここで紹介している内容は17年3月時点の情報です。ご紹介している内容・名称等は変わることがあります1 辺(h) 3 2 底面積(S) 4 3 側面積(F) =1/3*B1*B2 角錐台 計算 辺(a) 辺(b) 高さ(h) 体積 \ V = \frac{h}{3} ( TB \sqrt{TB}) \ EXCELの数式 A B;円錐の体積の求め方 公式と計算例 Scipursuit 体積の求め方 円錐 円錐の体積を求める公式は、次の通りです。 V = 1 3Sh = 1 3πr2h V = 1 3 S h = 1 3 π r 2 h ここで、V は円錐の体積、S は底面積、h は高さを表します。 また、2行目における π は円周率、r は底面の

どうして1 3なの 錐の体積の公式の求め方 まなべーと

Studydoctor柱体や角錐の表面積の求め方 中学１年数学 Studydoctor

 三角柱の体積の求め方へ 底面積×高さ と同じ値になるということを抑えます。 飽くまでも同じなのは体積の値であり、考え方ではありません。 これで、三角柱の体積は、底面積×高さ で求められる！ としてはいけません。今、扱ったのは、底面が直角四角錐の体積の求め方 四角錐の体積は、底面積を S 、高さを h とした場合、 1/3 Sh で求められます。 四角錐の底面は、長方形や平行四辺形など、どんな四角形でも 1/3 Sh で体積を求められます。 導出方法 立方体を区切って、以下のように、6つの四角錐を作ります。四角錐の体積を1とすると、立方体の体積は6です。1 高さ(h) 3 2 上面積(T) 4 3 底面積(B) 5 4 体積(V) =/3*(B1B2

円錐の体積の公式 死ぬほど問題に出るので求め方を絶対に覚えよう 中学や高校の数学の計算問題

3

11月26日（火） 角錐の体積の求め方 6年生の算数の授業です。 角錐・円錐の体積の求め方には底面積×高さ÷3という公式があります。 「なぜ、÷3するのか」という疑問を解決するために、四角錐などの立体を組み合わせて考えました。 自分たちが体積を 上述のように、体積比の求め方は辺の長さの比を3乗すればいいので、2^3：7^3＝8：343と変換されました。 今度は逆に体積比から辺の長さの比を求めていきましょう 例題 ある相似な三角錐二つの体積比は、1：27です。このときの、二つの立体図形の相似比は 中学 理科の問題 水蒸気量の求め方 テストで水蒸気量の求め方という問題が出るそうです 飽和水蒸気量と湿度から求める問題が出ると言っていました これはグラフからの読み取りでしょうか？文章でしょうか？ 求め方も説明してくださるとありがたいです

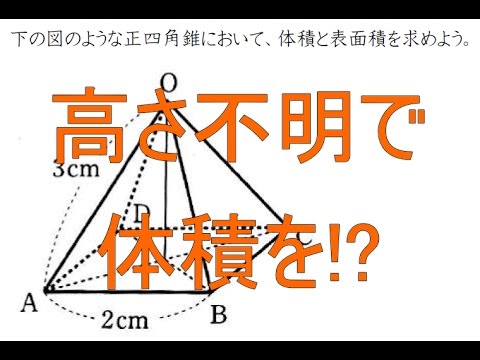
正四角錐と三平方の定理 中学３年数学 Youtube

正五角錐の体積の求め方 理系のための備忘録

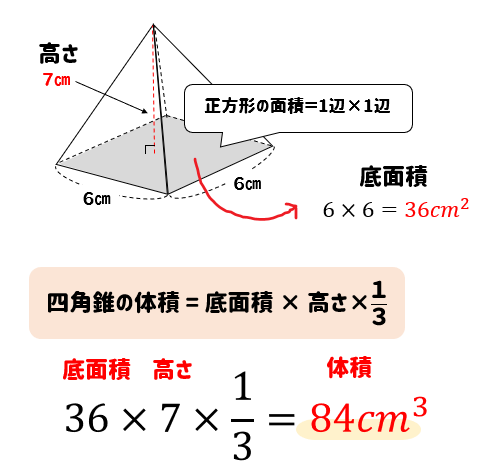
数学三角錐の体積比を楽に求められる公式 ～受験の秒殺テク（2）～ キーワードは"ちぢみ率" 高校受験を控える中学3年生の皆さんに、わずかな時間で正解を出すことができる"秒殺テクニック"を紹介していきます。（問1）次の角錐の体積を求めなさい。 （1）正四角錐 底面積(1辺が6cmの正方形の面積) 1 3 ＝84 高さ 答 84cm3 （2）正五角錐 底面積(底面の正五角形の面積) 1 3 ＝140 ＝ 高さ 5 答 140cm3 ただし、底面の五角形の 面積は42cm2である。 （例2）次の円錐の体積を求 めなさい。 （解答） 円錐の体積三種類の公式 0：13 まずは立体の体積を求める公式を確認しましょう。 角柱・円柱 底面積 × 高さ 角錐・円錐 底面積 × 高さ × 1 3 球 4 3 × π × r 3 3 種類の公式を使い、いろいろな立体の体積を求めてみましょう。

簡単 三角錐の体積 表面積の求め方と展開図が誰でもすぐわかる記事 高校生向け受験応援メディア 受験のミカタ

三角錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典

四角錐の体積の求め方\(1\)\(2\) 求め方 ・ 公式\(\frac{1}{3}Sh\)に底面積と高さを代入する ・ 底面積は\(35\)、高さは\(5\) ・ 四角錐の体積\(\hskip2pt=\frac{1}{3}\times35\times5=\frac{175}{3}\) 答え \(\frac{175}{3}\mathrm{cm^3}\) 四角錐の体積の求め方・まとめ 四角錐の体積を求めるときは、公式\(\frac{1}{3}Sh\)に底面積と高さを代入しましょう。 では、円錐・角錐などの錐体の体積は「底面積×高さ÷3」ですが、 なぜ3で割るのでしょうか？ 私が昔中学生の頃、へっぽこな数学教師にこれを質問したところ、 「きっと昔の人が円柱と円錐の容器に水を入れて、その量を比べて 3で割る事を発見したん 自分の計算としては下流面での四角錐台体積(649)から上下流の辺の差から求めた四角錐()を引いた484でした。発注者設計量は43㎥です。 ただ、現場で見る限り(垂直壁、側壁は施工済み)足りないように感じます。60㎥は入るように感じます。 計算違いでしょうか？ 経験者の方、数学強い

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

四角錐の体積の求め方 公式 小学生 中学生の勉強

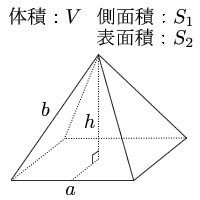
底辺の長さと高さを入力し「正四角錐の体積・表面積を計算」ボタンをクリックすると、正四角錐の体積・表面積・斜辺の長さを計算して表示します。 底辺の長さ a： 高さ h： 底辺の1辺の長さaが2、高さhが3の正四角錐の体積・表面積・斜辺の長さ 体積 V：4 側面積 S 1 ： 表面積 S 2 中学生で習う円錐と角錐の体積。底面積が\(S\)、高さが\(h\)の円錐・角錐の体積\(V\)は下記の式で表されます。 $$V=\displaystyle \frac{3}{1}Sh$$ 円柱と角柱の公式が、\(V=Sh\)なので、なんで\(\displaystyle \frac{1}{3}\)が付くの？と疑問に思いますよね。 四角錐の体積＝底面積×高さ× 1 3 より 四角錐の高さ＝四角錐の体積÷底面積×3で求めることが出来ます。 ここで、底面積＝12×12＝144（cm²）であることから 求める四角錐の高さ＝432÷144×3＝9（cm）となります。 答え 9cm ～立体の体積・表面積を求める公式まとめ～ 立方体・直方体の体積の求め方公式 円柱の体積の求め方公式

なぜ 錐体 は3で割る 簡単な説明を 正多面体 から伝授します 横山 明日希 ブルーバックス 講談社 3 4

１１月２６日 火 角錐の体積の求め方 ノートルダム学院小学校

正四角錐の体積（底辺と高さから） 正四角錐の体積（底辺と側辺から） 正四角錐台の体積 四角錐台の体積 くさび形の体積 角錐台の体積 角錐の体積 直円柱の体積 一部が欠けた直円柱の体積 中空円柱の体積 斜切円柱の体積 楕円柱の体積 直円錐の体積 斜切円錐の体積

角錐 円錐の体積と表面積の公式 数学fun

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 Hatsudy 数学 科学

3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

正四角錐 底辺と高さ 体積 表面積の計算 計算サイト

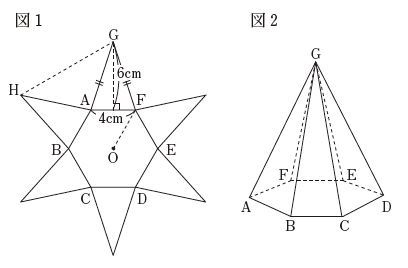
線分hgの長さ 六角錐の体積 中3から質問へのヒント 上北沢 哲英会 個人塾 連絡用ブログ

どうして1 3なの 錐の体積の公式の求め方 まなべーと

角錐 円錐の体積と表面積 計算ドリル 問題集 数学fun

四角錐の体積の求め方 公式 小学生 中学生の勉強

3分でなるほど 三角錐の体積 表面積の求め方をマスターしよう 数スタ

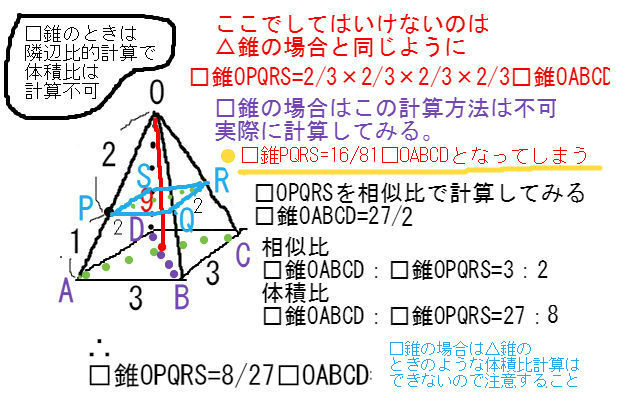
三角錐と四角錐の体積比計算方法の違い 中学 数学 理科の復習サイト

数学 中3 68 三平方 空間図形への利用 角錐編 Youtube

角錐と円錐の体積の求め方は 同じなんですか 円錐が底面 高さ Yahoo 知恵袋

四角錐の表面積の求め方 公式 小学生 中学生の勉強

3分で分かる 三角錐の体積 表面積の求め方 公式 練習問題 についてわかりやすく 合格サプリ

円柱の表面積の求め方

体積の求め方 計算公式一覧

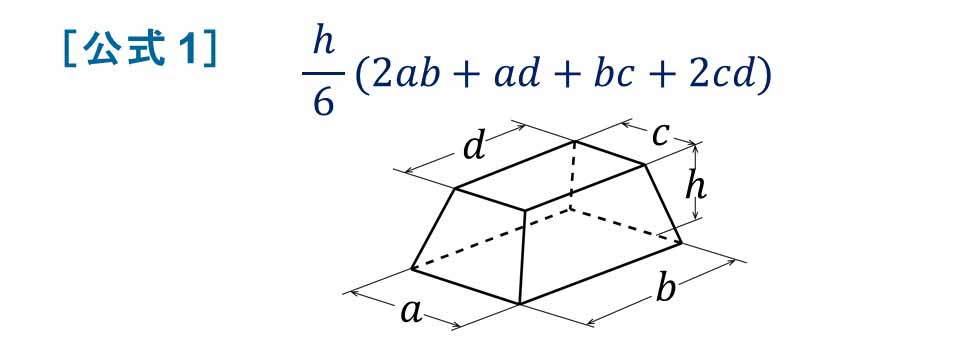
公式の証明 体積測定によって検証する土塁の取崩しと土橋の造成

四角錐の表面積の求め方 公式 小学生 中学生の勉強

体積の求め方 計算公式一覧

三平方の定理の利用 四角錐 円錐 チーム エン

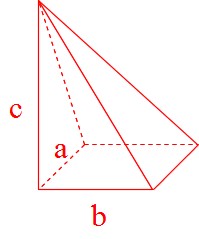
Mathematics 角錐の体積が角柱の３分の１になる証明 働きアリ

三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

3分で分かる 円錐の体積 表面積の求め方をわかりやすく 合格サプリ

正四角錐の体積の求め方や高さの求め方などがわかりません教えてください Yahoo 知恵袋

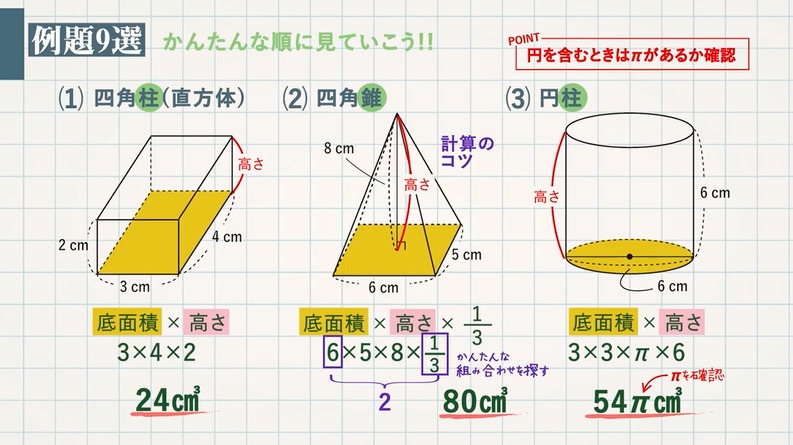
立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

この問題を教えてください 六角錐の体積の求め方の公式なんてないです Yahoo 知恵袋

角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

角錐 円錐の体積と表面積の公式 数学fun

四角錐の体積の求め方 公式 小学生 中学生の勉強

四角錐の体積の求め方 公式 小学生 中学生の勉強

正五角錐の体積の求め方 理系のための備忘録

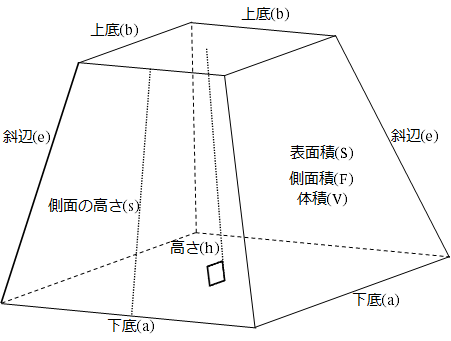
Excelワークシート 正四角錐台の体積や表面積などを計算するワークシート 黒い箱の中

3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

立体の体積 無料で使える中学学習プリント

角錐の体積の公式は 1分でわかる公式 柱体の体積との違い 3分の1になる証明

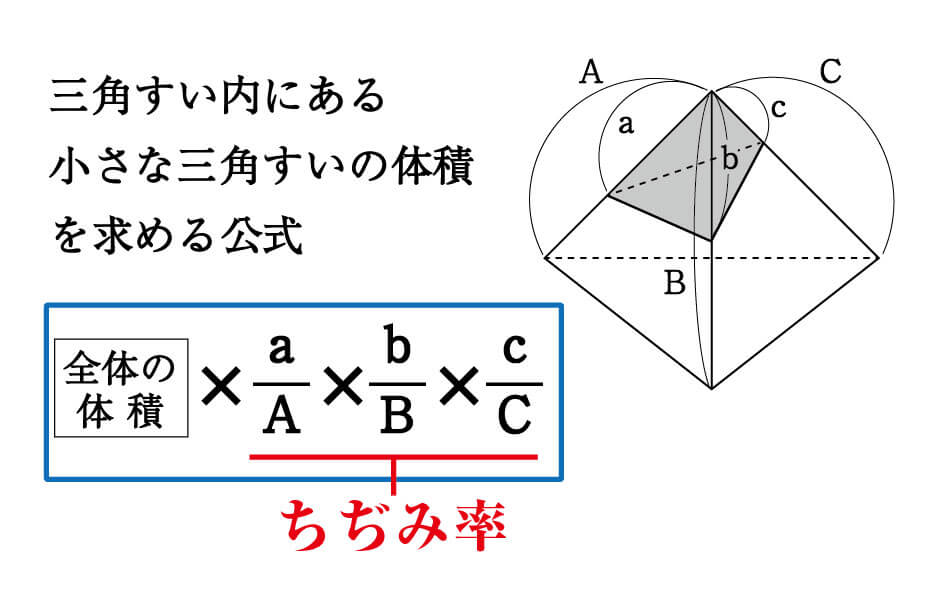
数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

四角錐台の体積 高精度計算サイト

三角錐 四面体 の体積の公式 Schoolmath S Diary

角錐の体積の求め方 簡単な問題で公式の使い方がわかるよ 中学や高校の数学の計算問題

計算公式 正四角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

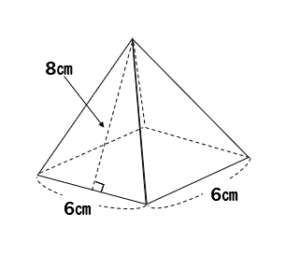
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

この写真の正四角錐の高さの求め方教えてください 四角錐の体積の公式 Yahoo 知恵袋

円錐 すい の表面積や四角錐 五角錐の体積の求め方

体積の求め方 計算公式一覧

高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

簡単公式 三角錐の体積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

角錐 円錐の体積と表面積の求め方 錐体の公式と母線の概念 Hatsudy 数学 科学

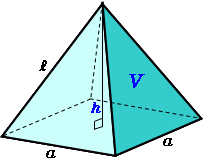
正四角錐の体積 底辺と側辺から 高精度計算サイト

角錐 円錐の体積と表面積の公式 数学fun

正四角錐台の体積の求め方 Media Qikeru Yahoo 知恵袋

三角錐と四角錐の体積比計算方法の違い 中学 数学 理科の復習サイト

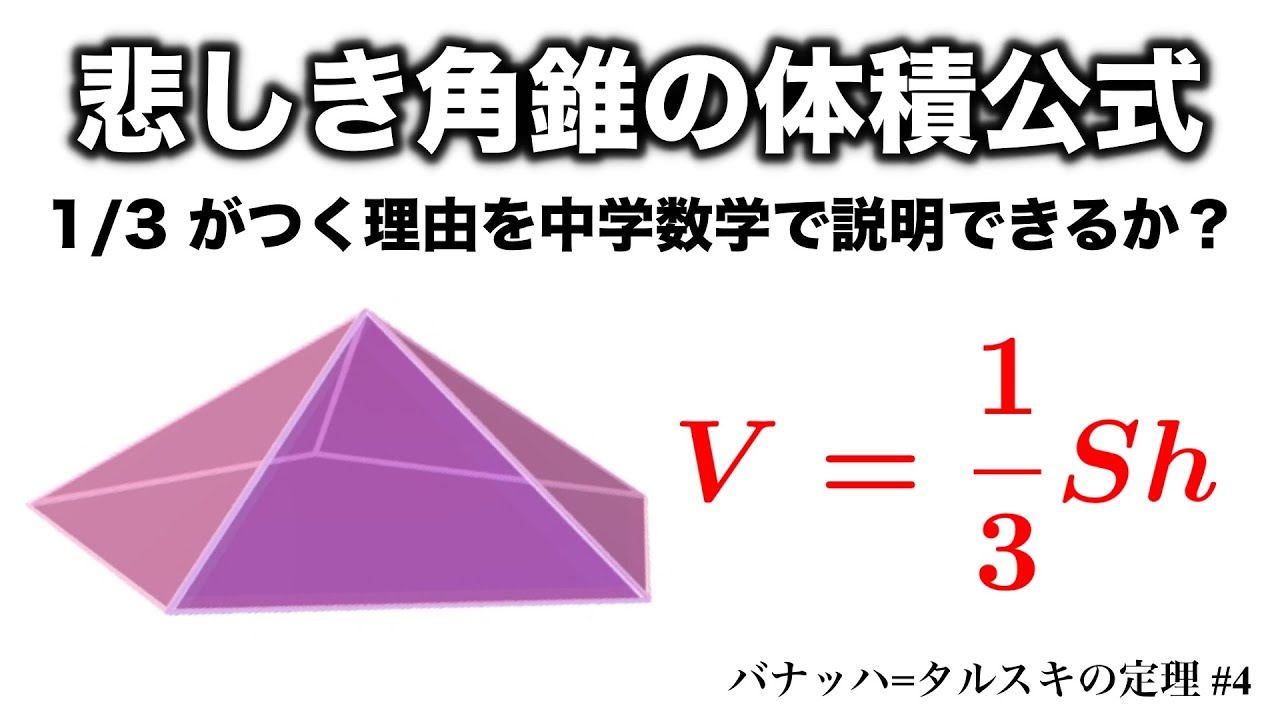
悲しき角錐の体積公式 1 3 がつく理由を中学数学で説明できる バナッハ タルスキーの定理 4 Youtube

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

1

公式を図解 すい体の体積 円すいの表面積 の公式の求め方と使い方 中学受験ナビ

Studydoctor円錐や角錐の体積の求め方 中学１年数学 Studydoctor

台形の体積 って何 相似の考え方を利用して四角錐台の体積を求めよう 中学受験ナビ

中1数学 三角すい 四角すいの体積の求め方がサクッとわかる 映像授業のtry It トライイット

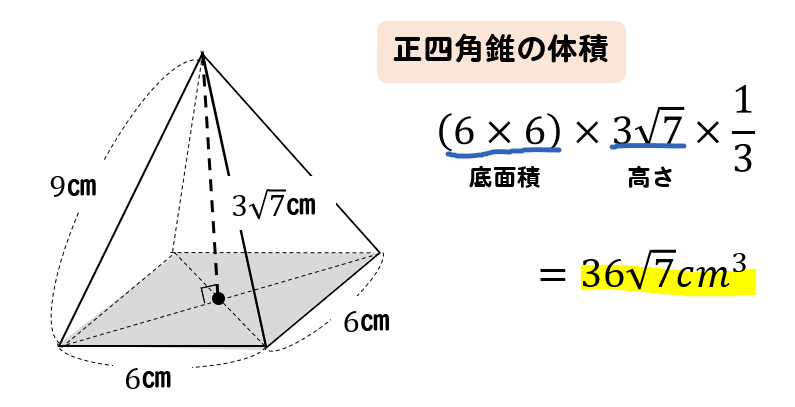
高さの分からない正四角錐の体積を求める方法をイチから解説 数スタ

旧ver 7分でわかる 角錐 円錐 表面積 体積 について徹底解説します 中1数学 Youtube

三角錐とは 体積 表面積の公式や求め方をわかりやすく解説 受験辞典

角錐 円錐の体積と表面積の公式 数学fun

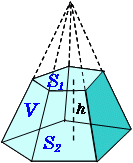
角錐台の体積 高精度計算サイト

答953 正六角錐の体積と表面積 解答集

Android 用の 体積計算 Bynsdev Apk をダウンロード

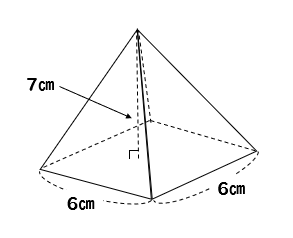
3分でなるほど 四角錐の体積 表面積の求め方をマスターしよう 数スタ

円錐の表面積や体積の求め方 すぐ分かる方法を慶応生が解説 高校生向け受験応援メディア 受験のミカタ

下のような四角錐台の体積の求め方をわかりやすく教えてください A ５b ３ Yahoo 知恵袋

角錐 円錐の体積 Youtube

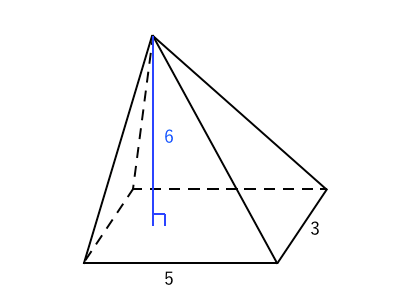
超簡単 体積の求め方 苦手な数学を簡単に

円錐の表面積の求め方 裏技の公式を覚えたらめちゃくちゃ簡単 中学や高校の数学の計算問題

錐体の体積に1 3がつくことの２通りの説明 高校数学の美しい物語

6分でわかる 角錐 円錐 表面積や体積の求め方 中1数学 Repost 再編集済み Youtube

数学 三角錐の体積比を楽に求められる公式 受験の秒殺テク 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo

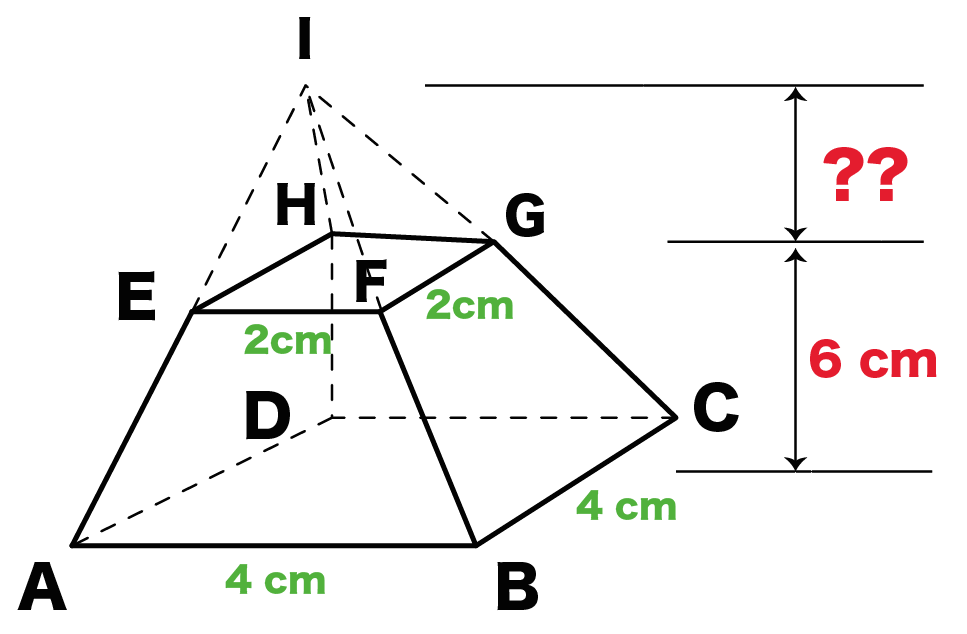
簡単公式 台形の体積 正四角錐台 の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく

四角錐 円錐の体積 チーム エン

立体の体積まとめ 角柱 円柱 角錐 円錐 球 A 教遊者

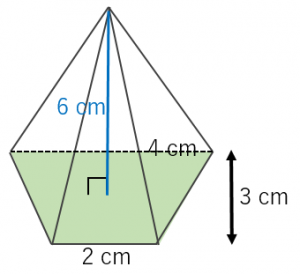
三角錐 四角錐 円錐の体積を求める公式と例題 具体例で学ぶ数学

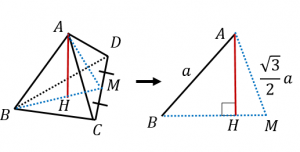
正四面体の高さと体積の求め方 具体例で学ぶ数学

角柱 円柱の表面積と体積の公式 数学fun

Incoming Term: 角錐 体積 求め方,